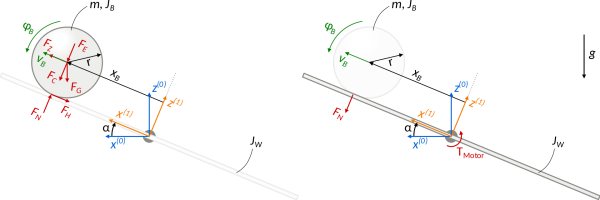
The ball and beam system is more or less what is sounds like. A ball is located on a beam and the objective is to place the ball at a given position on the beam, or to have the ball follow a specific linear trajectory along the beam. Videos can be found on youtube ( here and here) of simple versions running off of an RC servomotor. The linked videos are the indirect control design, which uses a leverl between the motor and the beam. As obtained from wikipedia, the traditional design is depicted below, with the ball modeling emphasized on the left half of the image and the beam modeling emphasized on the right half.

This project is a bit like the inverted cart-pundulum system, in terms of being single input, except that the nonlinearities are matched. The extended version with the motor or possibly beam dynamics does have unmatched nonlinearities.

I will know better the structure as we work out this system. Depends on a student group who proposed it passing me starter equations.

The energy of the system is \begin{equation} \mathcal{E} = \frac 12 \left(J_B + J_b\right){\dot \theta}^2 + \frac 12 m_b x^2 {\dot \theta}^2 + \frac 12 \left(m_b + \frac{J_b}{r^2}\right) \dot x^2 + m_b g x \sin(\theta), \end{equation} while the Lagrangian (kinetic minus potential energies) is \begin{equation} \mathcal{L} = \frac 12 \left(J_B + J_b\right){\dot \theta}^2 + \frac 12 m_b x^2 {\dot \theta}^2 + \frac 12 \left(m_b + \frac{J_b}{r^2}\right) \dot x^2 - m_b g x \sin(\theta). \end{equation}

If the beam angle, $\theta$, dynamics are ignored, then the dynamics for the system simplify to a second order nonlinear model. The equations of motion for the ball position depend on the angle of the beam, \begin{equation} \left( m_b + \frac{J_b}{r^2} \right) \ddot x - m_b {\dot \theta}^2 x + m_b g \sin(\theta) = 0. \end{equation} These equations rely on the inertia of the beam being negligible and the beam angle $\theta$ being precisely controlled.

Variables: \begin{equation} \begin{split} m & = 0.111 \\ R & = 0.015; \\ g & = -9.8; \\ L & = 1.0; \\ % d = 0.03; J_b & = 9.99e^{-6}; \end{split} \end{equation}

The system can be made a little more complicated by considering the motor dynamics, presuming that a DC motor was the actuator, \begin{equation} \begin{split} J_m \ddot \theta & = K \iota - m_b g x \cos(\theta) - \dot \theta \\ L \dot \iota & = V - R \iota - K_e \dot \theta \end{split} \end{equation} where $\iota$ is the motor current, $V$ is the motor voltage, and some potential energy coupling from the ball/beam system is included in the motor angle dynamics.

Stabilization of the system would be to some value $(x^*, 0)$ where the ball is on the beam and presumably the beam is not angled. The simplest stabilization would be to some time-varying signal $(x^*(t), \dot x^*(t))$ like a sinusoid or some rsteps like function where the magnitude of $x^*(t)$ is reasonable and time rate of change is likewise reasonably bounded. At this point, you should be able to pick reasonable tracking objectives for demonstrating the outcomes of your controllers, adaptive or otherwise.

Linearize the system about the zero set-point and derive a stabilizing linear controller for the ball-beam system. Modify the parameters by about 20%, and show how the performance degrades versus knowing the ideal model. Create an adaptive controller that can improve the overall performance of the ball-beam system.

Create a nonlinear adaptive controller that can improve the overall performance of the ball-beam system.

The nonlinearieties lie in the span of the control. Rewrite the equations so that this is the case and make sure to include the control defect in the equations arising from the sine function. Utilize a model inversion / feedback linearization technique on the true nonlinear system to arrive at a stable controller for the ball-beam system. I am going to request something funny. Add two additional states that will estimate $\theta$ and $\dot \theta$ given a measured input of $\theta = u$, the control. The estimator equations should be the trivial second order dynamics. These two additional states will be tacked onto the adaptive system and will be used for the nonlinear regression problem associated to the model inversion cancelling term. The parametrization is known in this case.

Turn in your form of the equations for this particular case and the associated adaptive control equations. Again, compare the perturbed system versus the true system response.

Add in the motor dynamics and have them be linearized around the steady-state. Work out what steady-state should be for a given non-zero target ball position $(x^*, 0)$. Have your trajectories also be relative to this position so that the linearization remains valid. Work out a good controller for this fifth order system. Remember that you are controlling $x$ via $\theta$ which is controlled through $I$ which has the control $V$.

This linear system is looking a lot like a backstepping control, but where backstepping is usually not applied because the system should be controllable in the linearization. You can try to work out a backstepping approach for the linearized dynamics if that seems most sensible. You should relate to a linear controller though to continue.

Incorporate adaptive control to correct for the unmatched uncertainty. Randomly perturb by about 15% the parameters.

Translate the linear adaptive backstepping strategy to the nonlinear system. Start with the vanilla nonlinear backstepping method, then make it adaptive.

Consider the nonlinearities of the system and identify a backstepping approach to controlling the system. Get the baseline backstepping method working. It should resemble that of the linear controller from Step 2 but with nonlinear terms.

Add in adaptation to the backstepping controller, using the same 15% perturbed model.

Back – Main