Table of Contents
Ball and Beam System
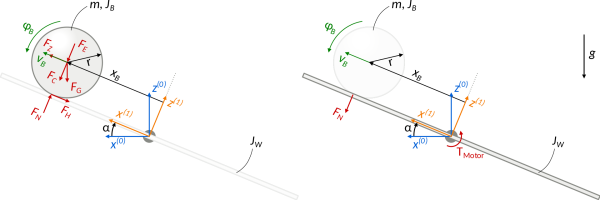
The ball and beam system is more or less what is sounds like. A ball is located on a beam and the objective is to place the ball at a given position on the beam, or to have the ball follow a specific linear trajectory along the beam. Videos can be found on youtube ( here and here) of simple versions running off of an RC servomotor. The linked videos are the indirect control design, which uses a leverl between the motor and the beam. As obtained from wikipedia, the traditional design is depicted below, with the ball modeling emphasized on the left half of the image and the beam modeling emphasized on the right half.
This project is a bit like the inverted cart-pundulum system, in terms of being single input, except that the nonlinearities are matched. The extended version with the motor or possibly beam dynamics does have unmatched nonlinearities.
I will know better the structure as we work out this system. Depends on a student group who proposed it passing me starter equations. 
Equations of Motion
The energy of the system is \begin{equation} \mathcal{E} = \frac 12 \left(J_B + J_b\right){\dot \theta}^2 + \frac 12 m_b x^2 {\dot \theta}^2 + \frac 12 \left(m_b + \frac{J_b}{r^2}\right) \dot x^2 + m_b g x \sin(\theta), \end{equation} while the Lagrangian (kinetic minus potential energies) is \begin{equation} \mathcal{L} = \frac 12 \left(J_B + J_b\right){\dot \theta}^2 + \frac 12 m_b x^2 {\dot \theta}^2 + \frac 12 \left(m_b + \frac{J_b}{r^2}\right) \dot x^2 - m_b g x \sin(\theta). \end{equation}
If the beam angle, $\theta$, dynamics are ignored, then the dynamics for the system simplify to a second order nonlinear model. The equations of motion for the ball position depend on the angle of the beam, \begin{equation} \left( m_b + \frac{J_b}{r^2} \right) \ddot x - m_b {\dot \theta}^2 x + m_b g \sin(\theta) = 0. \end{equation} These equations rely on the inertia of the beam being negligible and the beam angle $\theta$ being precisely controlled.
Variables:
| Parameter | Value |
|---|---|
| $m$ | 0.111 kg |
| $r$ | 0.015 m |
| $g$ | -9.8 m/s$^2$ |
| $L$ | 1.0 m |
| $J_b$ | 9.99e$^{-6}$ |
Adding Motor Dynamics
The system can be made a little more complicated by considering the motor dynamics, presuming that a DC motor was the actuator, \begin{equation} \begin{split} J_m \ddot \theta & = K \iota - m_b g x \cos(\theta) - \dot \theta \\ L_m \dot \iota & = V - R_m \iota - K_e \dot \theta \end{split} \end{equation} where $\iota$ is the motor current, $V$ is the motor voltage, and some potential energy coupling from the ball/beam system is included in the motor angle dynamics.
Variables: Variables:
| Parameter | Value |
|---|---|
| $J_m$ | 0.043 |
| $K$ | 4.91 |
| $L_m$ | 0.0016 |
| $R_m$ | 4.7 |
| $K_e$ | 4.77 |
Obtained from Wang (2007).
Stabilization and Tracking
Stabilization of the system would be to some value $(x^*, 0)$ where the ball is on the beam and presumably the beam is not angled. The simplest stabilization would be to some time-varying signal $(x^*(t), \dot x^*(t))$ like a sinusoid or some rsteps like function where the magnitude of $x^*(t)$ is reasonable and time rate of change is likewise reasonably bounded. At this point, you should be able to pick reasonable tracking objectives for demonstrating the outcomes of your controllers, adaptive or otherwise.
Activities
Step 1: Baseline Adaptive Systems
Linear Version
Linearize the system about the zero set-point and derive a stabilizing linear controller for the ball-beam system. Modify the parameters by about 20%, and show how the performance degrades versus knowing the ideal model. Create an adaptive controller that can improve the overall performance of the ball-beam system.
For this part, please run the versions with linear dynamics and with nonlinear dynamics. That means there will be four instances run based on the binary options of dynamics and adaptive control. Since your control $u(t)$ is $\theta(t)$, you will naturally not have access to $\dot \theta$. The way around this is to design the system in simulink and use a $d/dt$ block to obtain the derivative of the input for use as $\dot \theta$. Until you get to the later steps, where the dynamics of $\theta$ are utilized, you'll have to use this particular cheat.
Nonlinear Version
Create a nonlinear adaptive controller that should improve the overall performance of the ball-beam system. The nonlinearieties lie in the span of the control. Rewrite the equations so that this is the case and make sure to include the control defect in the equations arising from the sine function; basically try to think of the problem as a linear system plus a nonlinear defect. Provide the massaged equations of motion.
Utilize a model inversion / feedback linearization technique on the true nonlinear system to arrive at a stable controller for the ball-beam system. For the true dynamics, you will continue to utilize the Simulink model designed in the earlier step. For the nonlinear control terms, you will deny yourself access to the true signals and will have to generate them another way. To be able to do this, I am going to request something funny. Add two additional states that will estimate $\theta$ and $\dot \theta$ given a measured input of $\theta = u$, the control. The estimator equations should be the trivial second order dynamics. These two additional states will be tacked onto the adaptive system and will be used for the nonlinear regression problem associated to the model inversion cancelling term. The parametrization is known in this case.
Turn in your form of the equations for this particular case and the associated adaptive control equations. Again, compare the perturbed system versus the true system response. In this case the only binary variable is adaptive control, so I would expect to see two different types of runs. These runs should be performed with different types of signals, much like the homework stabilizes to a reference and tracks a target trajectory. Note that there is something of an algebraic loop in the problem as you are using the control to cancel out a nonlinearity due to the control. That means you should not be so aggressive regarding the adaptive gains for the nonlinear cancellations, and you might want to be have a bit more damping than normal for the drift prevention terms.
Step 2: Full Linear System (An Almost Backstepping Approach)
Motor Control: Linear
Add in the motor dynamics and have them be linearized around the steady-state. Work out what steady-state should be for a given non-zero target ball position $(x^*, 0)$ (it should be reasonably located, as in not too far out). Have your trajectories also be relative to this position so that the linearization remains valid. Work out a good controller for this fifth order system. Remember that you are controlling $x$ via $\theta$ which is controlled through $I$ which has the control $V$. Provide the $A$ and $B$ matrices.
This linear system is looking a lot like a backstepping control process, but where backstepping is usually not applied because the system should be controllable in the linearization. Since it is controllable in the linearization, all that is needed is to design a stabilizing controller for the fifth order system. Be careful about how quickly things stabilize as the main objective is to properly control the ball, then to control the beam.
Linear Adaptive Control
Incorporate adaptive control to correct for the unmatched uncertainty. Randomly perturb by about 15% the parameters. Since the uncertainty is unmatched, you will have to work out a backstepping type of adaptive control law. The uncertainty hits the $\dot x$, $\dot \theta$, $\iota$ coordinates dynamics. Provide your derivation of the adaptive control law, the final set of equations, and simulations showing it in action.
Tips: De-Coupled then Re-Coupled Adaptive Systems
Tip: Designing a fifth-order backstepping method is going to be pretty nasty, especially because of the dependency structure of things. Instead, decouple the system into two parts. One is the subsystem from Step 1 and the second is the new motor dynamics subsystem. Design a backstepping controller for the new motor dynamics subsystem independent of the ball subsystem. You will have to treat the ball signal as an external input in the decoupled system. Go ahead and do that when synthesizing the backstepping control policy for the motor subsystem. Get it to work out, then add on the adaptive ball system from Step 1. This is not 100% correct/ideal, but it is much simpler than attempting a full backstepping design that will end up with lord knows how many differentiated signals.
Tip: When designing the back-stepping type adaptive controller for the three new states, you should identify some candidate $x_1$ dynamics for the ball-beam part to be used in the motor controller. With $x_1$ specified in closed-form, the associated time derivatives can also be computed in closed form. These should be used as exogenous signals in the linear, back-stepping type adaptive controller. Later, when combining with the adaptive controller for the ball sub-system, you'll be trying to track the desired adaptive control law for the motor sub-system.
Step 3: Nonlinear Adaptive Backstepping
This Step should not be done for ECE6554 Spring 2019. Only complete Steps 1 + 2.
Translate the linear adaptive backstepping strategy to the nonlinear system. Start with the vanilla nonlinear backstepping method, then make it adaptive.
Nonlinear Model Inversion with Backstepping
Consider the nonlinearities of the system and identify a backstepping approach to controlling the system. Get the baseline backstepping method working. It should resemble that of the linear controller from Step 2 but with nonlinear terms.
Nonlinear Model Inversion with Adaptive Backstepping
Add in adaptation to the backstepping controller, using the same 15% perturbed model.
References
- J. Hauser, S. Sastry, P. Kokotovic. “Nonlinear Control via Approximate Input-Output Linearization: The Ball and Beam Example.” IEEE Trans on Automatic Control, 37(3):392-398, 1992. IEEE Xplore
- W. Wang. “Control of a Ball and Beam System,” MS Thesis, University of Adelaide, 2007. pdf